tg-me.com/knowledge_accumulator/261
Last Update:
A Conceptual Explanation of Bayesian Hyperparameter Optimization for Machine Learning [2018]
Неделю назад я писал пост про Evolution Strategies. Напомню его область применения:
1) Есть не очень большое пространство параметров
2) Есть функция качества этих параметров, но нет доступа к каким-либо градиентам
Эта область применения не так уж и редко встречается в реальной жизни, и чаще всего это происходит в контексте оптимизации гиперпараметров. В этом случае появляется ещё одно обстоятельство:
3) Функцию качества очень долго и дорого считать
В данной ситуации мы хотим максимально эффективно использовать этот ресурс, извлекать и переиспользовать максимальное количество информации из её замеров. Стандартный Evolution Strategies в этом плане достаточно туп - каждая итерация алгоритма происходит "с чистого листа", а точки для замера выбираются с помощью добавления шума.
Именно здесь на сцену выходит Bayesian model-based optimization. Это целое семейство методов, но все они работают по примерно одному и тому же принципу:
1) Мы пытаемся аппроксимировать распределение P(objective | params)
2) Мы используем каждое наше измерение для обучения этой аппроксимации
3) Выбор следующих кандидатов происходит по-умному, балансируя между неисследованными областями в пространстве параметров и проверкой тех областей, в которых мы ожидаем получить хорошее значение функции
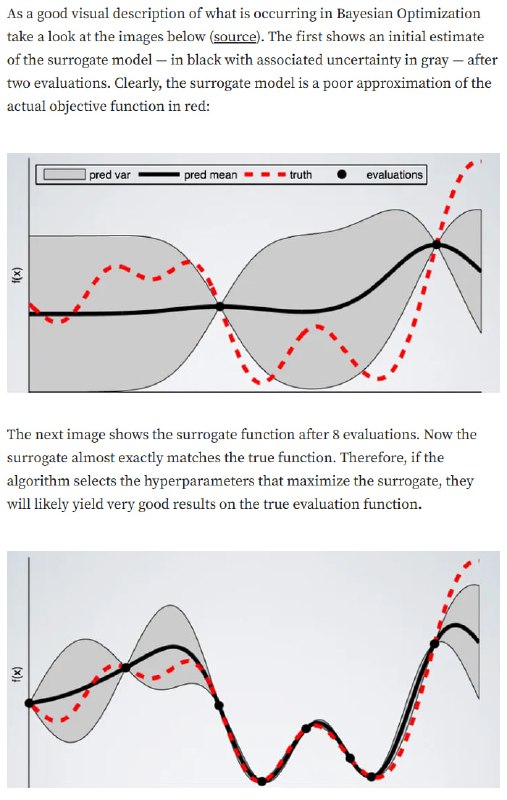
Исследуя всё больше и больше точек, мы получаем всё более точную аппроксимацию функции, как показано на картинке. Остаётся выбрать, каким образом моделировать распределение и выбирать кандидатов.
Один из вариантов, используемых на практике, выглядит так:
- При выборе следующих кандидатов мы максимизируем нечто похожее на "мат. ожидание" P(objective | params), но интеграл берётся только по "хорошим" значениям objective - это называется Expected Improvement
- Для оценки P(objective | params) мы формулу Байеса и переходим к моделированию P(params | objective), которое в свою очередь является композицией из двух распределений P(params) - для "хороших" значений objective и для "плохих" - эти распределения называется`L(params) и `G(params).
- В пунктах выше я упоминал "хорошие" и "плохие" значения. Порог, который их разделяет, выбирается как квантиль уже собранного нами множества значений objective.
При применении капельки математики получается, что Expected Improvement максимизируется в тех точках, в которых максимизируется` L(params) / G(params). Эти точки мы пытаемся найти, сэмплируя много раз из `L(params) и пересчитывая это соотношение. Вся эта схема называется Tree-structured Parzen Estimator.
Описанная процедура гораздо хитрее и тяжелее, чем Evolution Strategies, но всё это несопоставимо дешевле и быстрее, чем каждый подсчёт значения Objective(params). Таким образом, метод хорошо подходит для таких ситуаций, как оптимизация гиперпараметров обучения, и используется в качестве одного из основных в библиотеке Hyperopt.
Метод, конечно, не идеален - он не учитывает зависимости параметров между собой. Это может ограничивать область применения и мешать методу работать для оптимизации более запутанных схем. Бесплатные обеды, как обычно, не завезли.
@knowledge_accumulator
BY Knowledge Accumulator
Share with your friend now:
tg-me.com/knowledge_accumulator/261
